In making the move to Grade 3/4 a whole new world of curriculum landed in my lap. Since I had never taught double and triple digit multiplication before, I naturally began to teach my students how to do it in exactly the way that I learned how. There is definitely nothing wrong with the algorithm method, but over time I found it very helpful to learn a few other methods of approaching these problems. This post is dedicated to my new favorite…. the Box Method!
The first step of the box method is to draw a box. If you are multiplying two digits by two digits, your box should be two rows by two columns. A three digit by two digit problem would require three rows and two columns, or two rows by three columns (either way works because of the commutative property).

Next you expand each of the factors according to place value. So 24 becomes 20 + 4 and 35 becomes 30 + 5. Each part of the expanded notation is written across either the top or side of the box.
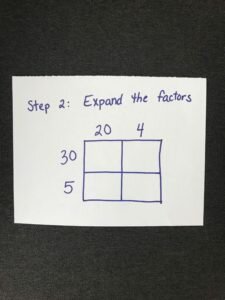
Step three is to multiply the numbers in the grid. This is just like a magic square. Multiply the top number by the side number and place the answer in the box where the row and column intersect. In this step I teach the kids how to multiply numbers that end in zero. I have them ignore the zeroes completely to start. So instead of worrying about 20 x 30, they just work on 2 x 3. Once they have written 6, they count up how many zeroes they ignored in the first place (2), and add these on, making 600. This really makes sense to them, and it covers another math standard in the process!

The last step is to add up all of the numbers in the box.

It’s as simple as that! Once the kids understand how to set up the box, they do remarkably well with this strategy. When teaching the Box Method I initially let the kids use a times table chart to help them. I am more concerned with them understanding the process of double or triple digit multiplication. Once they get the process, I give them problems to do without the chart, but I stick with numbers between 0 and 5 in all of the places. They are better at skip counting with the lower numbers and tend to know these lower times tables. The last “level” is to introduce larger numbers in the places. Once they can do problems like 89 x 76 I know that they understand the process and have a strong grasp on their times tables.
Here are a few other full examples:
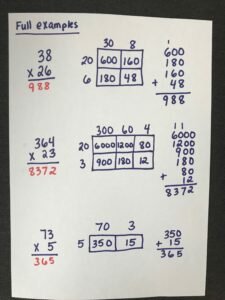
I plan on dedicating a few posts to other multiplication and division strategies I have learned over the past couple of years. Next up will be…. Partial Products!

Comments are closed.